Реализация ab initio подхода в молекулярной механике
Re: Реализация ab initio подхода в молекулярной механике
Все, теперь я этот момент ясно прочувствовал, спасибо огромное, madschumacher, amge и Shorku!
Re: Реализация ab initio подхода в молекулярной механике
Кроме D3 на HF могу еще вспомнить гриммовский HF-3c - туда вшиты и дисперсия и суперпозиционная ошибка.
Касательно происхождения ошибки - это да, возбужденные детерминанты, но небольшое число слейтеров достаточное для CASSCF не решает эту проблему и CASSCF иммет ровно такуюже недооценку дисперсии как ХФ.
МP2 - да, лечит, и даже перелечивает, у SCS-MP2, SOS-MP2, переоценка меньше, у MP3 легкая недооценка, вроде бы хорошо себя зарекомендовал MP2.5 это 50% MP2 и 50%виски MP3, но правильно наступит на CCSD
Касательно происхождения ошибки - это да, возбужденные детерминанты, но небольшое число слейтеров достаточное для CASSCF не решает эту проблему и CASSCF иммет ровно такуюже недооценку дисперсии как ХФ.
МP2 - да, лечит, и даже перелечивает, у SCS-MP2, SOS-MP2, переоценка меньше, у MP3 легкая недооценка, вроде бы хорошо себя зарекомендовал MP2.5 это 50% MP2 и 50%
Re: Реализация ab initio подхода в молекулярной механике
Доброй ночи, можно я со своим вопросом. Для этой структуры (симметрия Ci), насколько важны эффекты дисперсии?
И правильно ли я понимаю, что дисперсия приводит к стабилизации этого димера по сравнению с мономером?
И правильно ли я понимаю, что дисперсия приводит к стабилизации этого димера по сравнению с мономером?
У вас нет необходимых прав для просмотра вложений в этом сообщении.
Re: Реализация ab initio подхода в молекулярной механике
Очень важны. Если бы там не было карбоксил-металл взаимодействий то были бы доминантны. То есть B3LYP и B3LYP-D3 будут отличаться в разы (а возможно даже иметь разный знак, хотя это вряд ли катион-карбоксил наверняка дадут уже выгоду димеризации).
Да, дисперсия даст стабилизацию димера по сравнению с мономером.
Re: Реализация ab initio подхода в молекулярной механике
У меня такой вопрос: правильно ли понимаю, что молекулярная динамика обычно тоже ньютоновская, значит относительно простая? И если я сделаю молмеханику, смогу дальше перейти к молдинамике и это выглядит более перспективно.
Re: Реализация ab initio подхода в молекулярной механике
в первом приближении - да. Но посмотрите на это с другой стороны, у вас есть какой-то решатель - черный ящик. Как он реализован, ни кого не волнует. Вы знаете, что на входе у него - координаты атомов, а на выходе - энергия, иногда к энергии есть градиент этой энергии по координатам. Все, имея такую абстрактную сущность Вы сразу можете начинать молекулярно-динамить.
Так как мол-мех дает энергию и градиент существенно проще, то конечно с него проще начать и проще отлаживаться, но если все написать правильно, то у вас возникнет возможность потом перейти к DFT.
Re: Реализация ab initio подхода в молекулярной механике
Классическая молдинамика - на силовых полях (форсфилдовая).
Обычные силовые поля (GAFF) имплементируются (насколько я понимаю) намного проще чем DFT.
Для молдинамики кроме самой считалки вам еще нужен термостат. Термостатов разных много, имплементаций еще больше, я знаю что скажем madshumaher писал термостаты в свои коды.
Re: Реализация ab initio подхода в молекулярной механике
Сформулирую ещё раз свою задумку. Возьмём молекулу воды:
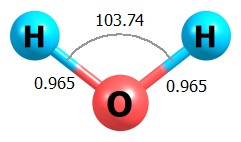
Здесь три степени свободы. Как я понимаю, для гармонического приближения не важно, брать ли три декартовы координаты либо угол и два расстояния; можно свободно пересчитывать силовые постоянные из одной системы координат в другую, результат не изменится. Возьмём второй вариант координат. ППЭ по углу в гармоническом приближении симметрично, т.е. если атомы водорода слипнутся, энергия станет такой же, как если разойдутся на эквивалентный угол (ну не совсем корректно сказал т.к. угол не может быть 180, но это другой момент). Мы же априорно знаем, что это не так - при слипнувшихся атомах энергия будет выше. Т.е. эту априорную информацию можно использовать, чтобы получить что-то получше стандартного гармонического приближения.
В гармоническом приближении мы имеем, если не путаю, суммарно 10 параметров: энергия, три градиента энергии и 6 силовых постоянных. Если по ним параметризовать 10 параметров ММ-модели, и дальше для этой ММ модели просчитать ангармонический спектр, то должно получиться лучше, чем в гармоническом приближении; насколько лучше - мы не знаем, может разница мизерная, а может существенная.

Здесь три степени свободы. Как я понимаю, для гармонического приближения не важно, брать ли три декартовы координаты либо угол и два расстояния; можно свободно пересчитывать силовые постоянные из одной системы координат в другую, результат не изменится. Возьмём второй вариант координат. ППЭ по углу в гармоническом приближении симметрично, т.е. если атомы водорода слипнутся, энергия станет такой же, как если разойдутся на эквивалентный угол (ну не совсем корректно сказал т.к. угол не может быть 180, но это другой момент). Мы же априорно знаем, что это не так - при слипнувшихся атомах энергия будет выше. Т.е. эту априорную информацию можно использовать, чтобы получить что-то получше стандартного гармонического приближения.
В гармоническом приближении мы имеем, если не путаю, суммарно 10 параметров: энергия, три градиента энергии и 6 силовых постоянных. Если по ним параметризовать 10 параметров ММ-модели, и дальше для этой ММ модели просчитать ангармонический спектр, то должно получиться лучше, чем в гармоническом приближении; насколько лучше - мы не знаем, может разница мизерная, а может существенная.
Re: Реализация ab initio подхода в молекулярной механике
ммм, ну...
гармоническое приближение говорит что если у вас минимум на 103 градусах энергия на 93 и 113 будет одинаковая.
формально конечно энергия на 179 (+76) и 27 (-76) градусах тоже совпадает, но с учетом квадратической зависимости - эти энергии настолько же велики насколько и бессмысленны. Они просто показывают что "отсюда надо срочно валить".
Ок, вы можете параметризовать 10-параметровую модель молекулы воды. На основе DFT или каких то иных высокоуровневых расчетов.
Но зачем? у вас уже 10 параметров но никакого учета межмолекулярки. 3-site модели используют для "геометрических целей" по сути 4 параметра, 5-site - 6 параметров, остальное это уже заряды. https://en.wikipedia.org/wiki/Water_model
Если же мы двинемся в системы бОльшего размера то нас очень быстро убьют ангармонические расчеты, а если не они - то число параметров в модели. Одновременно фитить 10 параметров - это уже задача не для счетов.
Возможно вы хотите в сторону "ангармонических поправок"? да, это тема модная, прикольная. По своему опыту скажу что ангармонические поправки играют сильнее там где малые силовые константы. Молекула воды отлично жесткая, соответственно ангармонизма там будет не так много, хотя смотря конечно куда смотреть. Вон смотрели 20 лет назад с применением MP2/6-311G** https://pubs.acs.org/doi/pdf/10.1021/j100087a008 - частоты улучшаются, интенсивности улучшаются но остаются хреновыми (ну то есть была переоценка 200%, стала переоценка 160% от эксперимента).
Re: Реализация ab initio подхода в молекулярной механике
Кажется я созрел до реальной работы над этой задачей, готов скоро приступить.
Как я уже писал, сейчас сделал программу, которая запускает программу xtb, та делает single point расчёт энергии и её градиентов, далее моя программа читает файл xtb и итерация повторяется.
Текущий алгоритм оптимизации крайне примитивный: к координатам атомов добавляются градиенты, умноженные на какой-то коэффициент. Если на следующем шаге энергия получилась ниже – система возвращается к предыдущим координатам, и этот коэффициент уменьшается.
Интересно сейчас получилось - такая молекула, как бензол, оптимизируется нормально, в то время как например пропан очень долго (если у пропана повернуть метильные группы вокруг связи C-C, они никак не соптимизизируются в правильное положение). Предлагаю догадаться, почему так получается.
Итак, каким у меня будет алгоритм: я сделаю кастомный ММ функционал, и его параметры будут динамически подгоняться под квантовохимический расчёт. Я не хочу изучать литературу по молекулярной механике, поскольку, как мне кажется, у меня лучше получится сразу придумать что-то своё. В моём алгоритме будут следующие параметры: три коэффициента для потенциала Морзе для каждой связи, и по два параметра для каждого атома, определяющих значения коэффициентов для потенциала Леннарда-Джонса с этим атомом, точнее определяющих как бы способность атома притягивать другие атомы с энергией, обратно пропонциональной шестой степени от расстояния, и отталкивать их с энергией, обратно пропорциональной двенадцатой степени. Понятно ли кому-то, о чём я говорю?
Возьмём для примера молекулу толуола:
Здесь 15 атомов и 15 связей. Значит суммарное число параметров будет 15*2+15*3=75. Эти параметры будут фиттиться на каждом шаге оптимизации.
Когда будет посчитана первая точка, расчёт даст только градиенты, т.е. этот расчёт покроет 15*3=45 степеней свободы (из них ещё 6 избыточных). Это значит, что фиттить ММ параметры неосторожно будет нельзя, иначе система улетит. Если же расчёт дойдёт до точки минимума и посчитаются частоты (вторые производные), он даст 45*46/2=1035 чисел, этого разумеется хватит для фита, и надо будет добавить ещё какие-то параметры, чтобы не недофитилось (недоиспользование данных расчёта частоты). Продолжение следует.
Как я уже писал, сейчас сделал программу, которая запускает программу xtb, та делает single point расчёт энергии и её градиентов, далее моя программа читает файл xtb и итерация повторяется.
Текущий алгоритм оптимизации крайне примитивный: к координатам атомов добавляются градиенты, умноженные на какой-то коэффициент. Если на следующем шаге энергия получилась ниже – система возвращается к предыдущим координатам, и этот коэффициент уменьшается.
Интересно сейчас получилось - такая молекула, как бензол, оптимизируется нормально, в то время как например пропан очень долго (если у пропана повернуть метильные группы вокруг связи C-C, они никак не соптимизизируются в правильное положение). Предлагаю догадаться, почему так получается.
Итак, каким у меня будет алгоритм: я сделаю кастомный ММ функционал, и его параметры будут динамически подгоняться под квантовохимический расчёт. Я не хочу изучать литературу по молекулярной механике, поскольку, как мне кажется, у меня лучше получится сразу придумать что-то своё. В моём алгоритме будут следующие параметры: три коэффициента для потенциала Морзе для каждой связи, и по два параметра для каждого атома, определяющих значения коэффициентов для потенциала Леннарда-Джонса с этим атомом, точнее определяющих как бы способность атома притягивать другие атомы с энергией, обратно пропонциональной шестой степени от расстояния, и отталкивать их с энергией, обратно пропорциональной двенадцатой степени. Понятно ли кому-то, о чём я говорю?
Возьмём для примера молекулу толуола:
Здесь 15 атомов и 15 связей. Значит суммарное число параметров будет 15*2+15*3=75. Эти параметры будут фиттиться на каждом шаге оптимизации.
Когда будет посчитана первая точка, расчёт даст только градиенты, т.е. этот расчёт покроет 15*3=45 степеней свободы (из них ещё 6 избыточных). Это значит, что фиттить ММ параметры неосторожно будет нельзя, иначе система улетит. Если же расчёт дойдёт до точки минимума и посчитаются частоты (вторые производные), он даст 45*46/2=1035 чисел, этого разумеется хватит для фита, и надо будет добавить ещё какие-то параметры, чтобы не недофитилось (недоиспользование данных расчёта частоты). Продолжение следует.
У вас нет необходимых прав для просмотра вложений в этом сообщении.
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 3 гостя